06 Sampling Distributions
Sampling¶
is used when it is not feasible to analyse the entire population
Population v Sample¶
| Property | Population | Sample |
|---|---|---|
| Definition | comprises of all units pertaining to a particular characteristic under study | is a part of a population, which is selected such that it is representative of the entire population |
| Size | \(N\) | \(n\) |
| Mean | \(\mu\) | \(\bar x = \dfrac {\sum x_i}{n}\) |
| Variance | \(\sigma^2\) | \(s^2 = \dfrac 1 {n-1} \left[ \sum {x_i}^2 - \dfrac { \left(\sum x_i \right)^2}{n} \right]\) |
| Standard Deviation | \(\sigma\) | \(s\) |
Relations¶
\[ \begin{aligned} E(\bar x) &= \mu, E(s^2) = \sigma^2 , E(s) = \sigma \\ s^2 &= \frac{\sigma^2}{n} , s = \frac{\sigma}{\sqrt n} \\ z_\text{sample} &= \frac{\bar x - \mu}{ \sigma/\sqrt n } \end{aligned} \]
Sample vs Population Standard Deviation¶
For Different Distributions¶
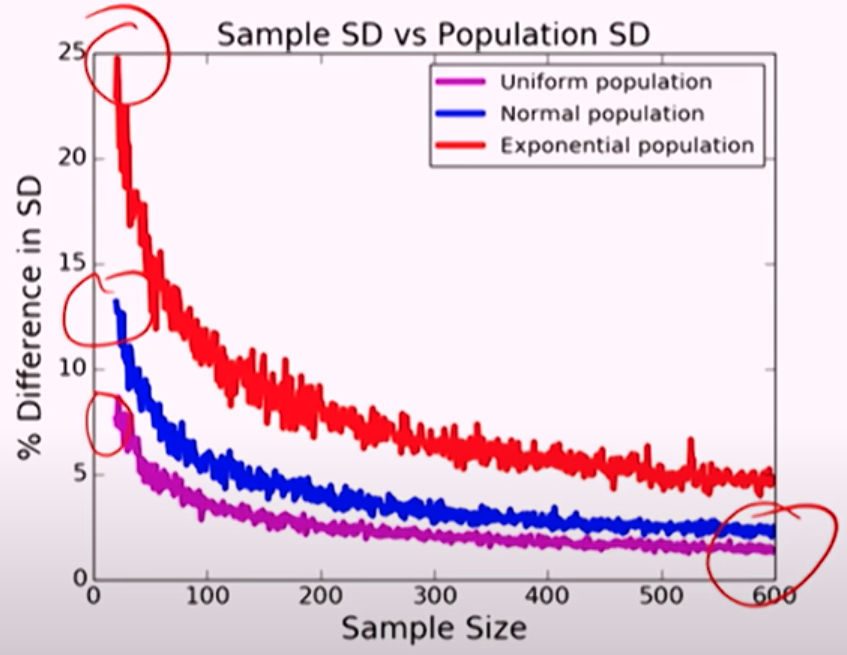
Higher the skew of population distribution, larger the sample size required to approximate the sample size to the population
For the different population size¶
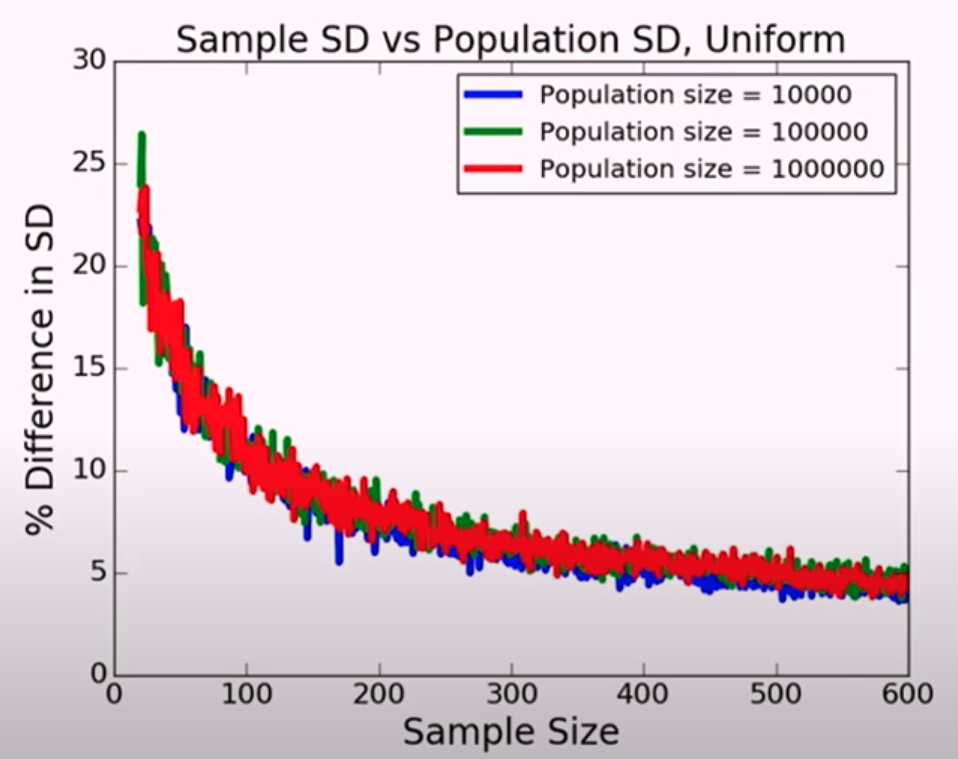
Sample vs Population SD does not depend on population size
Estimation¶
Using the sample, we estimate population parameter(s)
Interval Estimation¶
Confidence % \(= 1- \alpha\)
Most common is \(95\%\) confidence interval estimate
\[ \begin{aligned} 1 - \alpha &= 0.95 \\ \alpha &= 0.05 \\ \alpha/\small 2 &= 0.025 \end{aligned} \]
Population mean¶
| \(\sigma^2\) | \(n\) | statistic | \(\mu\) |
|---|---|---|---|
| known | any | \(z = \dfrac {\bar x - \mu}{\sigma / \sqrt n}\) | \(\bar x \pm z_{\alpha/\small 2} \cdot \dfrac \sigma {\sqrt n}\) |
| unknown | \(>30\) | \(z = \dfrac {\bar x - \mu}{s/ \sqrt n}\) | \(\bar x \pm z_{\alpha/\small 2} \cdot \dfrac s {\sqrt n}\) |
| unknown | \(\le 30\) | \(t = \dfrac {\bar x - \mu}{s / \sqrt n}\) | \(\bar x \pm t_{\small n-1, \alpha/\small 2} \cdot \dfrac s {\sqrt n} \\(n-1) \to \text{deg of freedom}\) |
\[ \begin{aligned} n &= \left( \frac{z_{\alpha/\small 2} \cdot \sigma}{w} \right)^2 \\ &= \left( \frac{z_{\alpha/\small 2} \cdot s}{w} \right)^2 \end{aligned} \]
where
- \(n\) is sample size
- \(w\) is distance from \(\mu\) = \(\frac{\text{interval width}}{2}\)
Proportion¶
\[ \begin{aligned} p &= \hat p \pm z_{\alpha/\small2} \sqrt {\frac{\hat p \hat q}{n}} \\ \hat p &= \frac x n = \frac{\text{Favorable no of cases}}{\text{Total no of cases}} \\ \hat q &= 1 - \hat p \end{aligned} \]
Population Variance / SD¶
\[ \begin{aligned} \sigma^2 &= \left[ \frac{(n-1)s^2}{\chi^2_{(n-1), (\alpha/\small 2)}}, \frac{(n-1)s^2}{\chi^2_{(n-1), (1-\alpha/\small 2)}} \right] \\ \sigma &= \sqrt {\sigma^2} \end{aligned} \]
Inequalities¶
Let \(x\) be a random variable such that \(x_i \in [a, b]\)
Consider
- sample size \(n\)
- \(\epsilon > 0\)
Hoeffding’s Inequality¶
\[ P (\vert \bar x − \mu \vert > \epsilon) \le 2 \exp \left[ \dfrac{-2 n \epsilon^2}{(b-a)^2} \right] \]
Vapnik-Chervonenkis Inequality¶
\[ P (\vert \bar x − \mu \vert > \epsilon) \le 4 \cdot m_h(2n) \cdot \exp \left[ \dfrac{-1}{8} n \epsilon^2 \right] \]
Where \(m_h(n) = 2^n\)