Skip to content

Recurrent Neural Networks

A recurrent neural network (RNN) is a kind of artificial neural network mainly used in speech recognition and natural language processing (NLP).

A recurrent neural network looks similar to a traditional neural network except that a memory-state is added to the neurons.

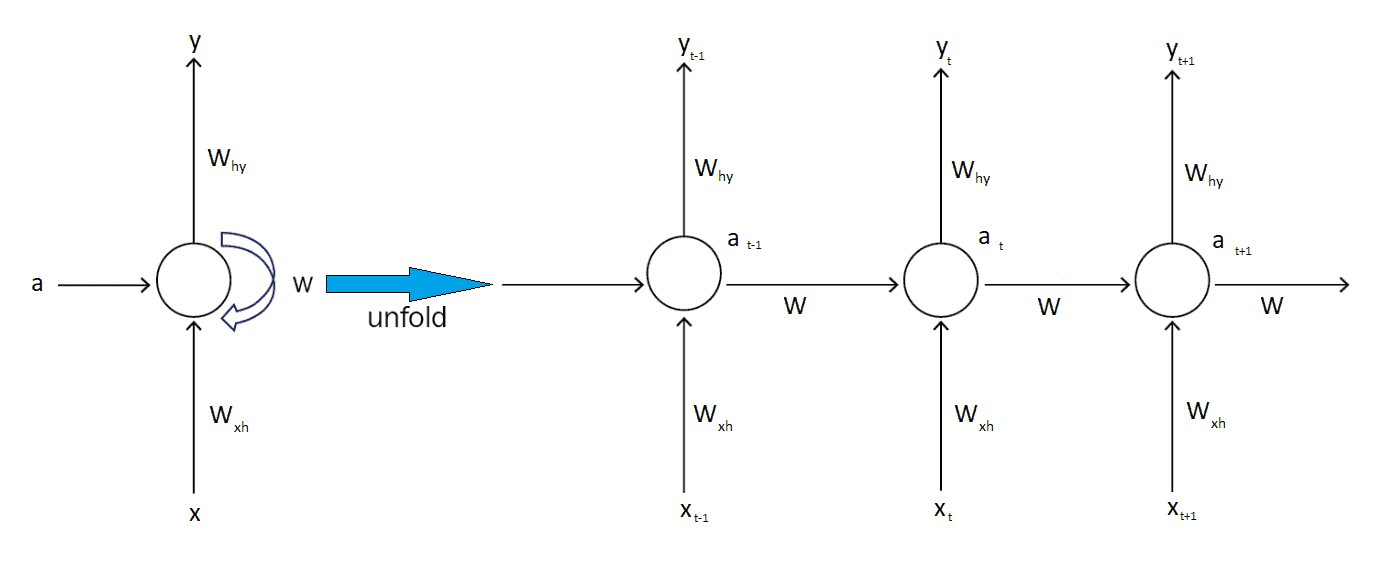
RNN diagram

image-20230529205211461

A RNN cell is a neural network that is used by the RNN.

As you can see, it’s the same cell repeats over time. The weights are updated as time progresses.

IDK

We introduce a latent variable, that summarizes all the relevant information about the past

image-20230527163547959

image-20230527163555542

\[ h_t = f(x_1, \dots, x_{t−1}) = f(h_{t−1},x_{t−1}) \]

Hidden State Update

\[ h_t = \phi \Big(W_{hh} h_{t−1} + W_{hx} x_{t−1} + b_h \Big) \]

Observation Update

\[ o_t = \phi(W_{ho} h_t + b_o) \]

Advantages

  1. Require much less training data to reach the same level of performance as other models
  2. Improve faster than other methods with larger datasets
  3. Distributed hidden state allows storage of information about pass efficiently
  4. Non-linear dynamics allows them to update their hidden state in complicated ways
  5. With enough neurons & time, RNNs can compute anything that can be done by a computer
  6. Good behaviors
  7. Can oscillate (good for motor control)
  8. Can settle to point attractors (good for retrieving memories)
  9. Can behave chaotically (bad for info processing)

Disadvantages

  1. High training cost
  2. Difficulty dealing with long-range dependencies

An Example RNN Computational Graph

image-20230527175223766

Implementing RNN Cell

image-20230529214150388

Tokenization/Input Encoding

Map text into sequence of IDs

image-20230527164906649

Granularity

Granularity ID for each Limitation
Character character Spellings not incorporated
Word word Costly for large vocabularies
Byte Pair Frequent subsequence (like syllables)

Minibatch Generation

Partitioning Independent samples? No need to reset hidden state?
Random Pick random offest
Distribute sequences @ random over mini batches		 ✅ ❌
Sequential Pick random offeset
Distribute sequences in sequence over mini batches		 ❌ ✅
(we can keep hidden state across mini batches)

Sequential sampling is much more accurate than random, since state is carried through

Hidden State Mechanics

  • Input vector sequence \(x_1, \dots, x_t\)
  • Hidden states \(h_1, \dots, x_t\), where \(h_t = f(h_{t-1}, x_t)\)
  • Output vector sequence \(o_1, \dots, o_t\), where \(o_t = g(h_t)\)

Often outputs of current state are used as input for next hidden state (and thus output)

Output Decoding

image-20230527165223776

\[ P(y|o) \propto \exp(V_y^T \ o) = \exp(o[y]) \]

Gradients

Long chain of dependencies for back-propagation

Need to keep a lot of intermediate values in memory

Gradients can have problems

Accuracy

Accuracy is usually measured in terms of log-likelihood. However, this makes outputs of different length incomparable (bad model on short output has higher likelihood than excellent model on very long output).

Hence, we normalize log-likelihood to sequence length

\[ \begin{aligned} \pi &= - \textcolor{hotpink}{\frac{1}{T}} \sum_{t=1}^T \log P(y_t|\text{model}) \\ \text{Perplexity} &= \exp(\pi) \end{aligned} \]

Perplexity is effectively number of possible choices on average

Truncated BPTT

Back-Propagation Through Time

Truncation Style
None Costly
Divergent
Fixed-Intervals Standard Approach
Approximation
Works well
Variable Length Exit after reweighing
Doesn’t work better in practice
Random Variable image-20230527174146972

image-20230527173745367

Last Updated: 2024-05-12 ; Contributors: AhmedThahir

Comments