Generalization¶
The ability of trained model to be able to perform well on unseen data. Better validation result \(\implies\) Better generalization
The generalization gap (error difference b/w seen and unseen data) should be small
The more models you try, the worse your generalization wrt that data due to increase in \(\vert H \vert\) as \(H = \bigcup_i H_i\) where \(H_i\) is the \(H\) for each model. This is the essence behind importance of train-dev-val-test split
Note: Always try to overfit with a very small sample and then focus on generalization
where
- \(\Omega =\) Overfit/Complexity Penalty
Lesson: Match the ‘model complexity’ to the data resources, not to the target complexity, ie, pick a hypothesis set that you can afford to navigate for the given training dataset
Noise¶
Part of \(y\) we cannot model
Types¶
| Stochastic/ Bayes’ Error | Deterministic | |
|---|---|---|
| Given by | \(u\) | \(f^* - f\) |
| Meaning | Observational error | Part of \(f\) that \(H\) cannot capture, even when there is no stochastic noise |
| Cause | \(P(y \vert x)\) | 1. Complexity of \(f\) 2. \(H\) |
| Frequency | High | Low |
| Smooth | ❌ | ✅ |
| For a given \(x\) | Randomly distributed | Fixed constant |
| Comment | No point trying to capture it, as you will learn a false pattern, given limited training dataset | |
| When teaching a kid, better to use easy-to-understand examples rather than the actual science | ||
 | ||
| Effect on overfitting |  |  |
- For a finite \(n\), \(H\) tends to fit both stochastic and deterministic noise
- Deterministic and Stochastic noise affect the Variance by making the model more susceptible to overfitting
- In presence of stochastic and/or deterministic noise, it is better to prefer smoother/simpler hypotheses, so that the model can avoid fitting the noise
-
For time-series modelling, we can use averaging/smoothing filter a pre-processing step
-
For target \(f\) of high complexity, train model \(\hat f\) with smooth \(\tilde y\) (for eg: Moving Average) to reduce effect of deterministic noise
Error Decomposition¶
| Bias | Variance \(\text{Var}(\hat f)\) | Distribution Mismatch | |
|---|---|---|---|
| Indicates | Inaccuracy | Imprecision | Data Sampling Issue |
| Meaning | Proximity of prediction is to true values | Amount by which \(\hat y\) would change for different training data | |
| Implication | Underfitting | Overfitting | |
| Denotation | \(\hat f-f\) | \(E \Big[ \ (\hat f - f^*)^2 \ \Big]\) | |
| Estimated through | Train Error - Acceptable Error | Dev error - Train Error | Validation Error - Dev Error |
| Reason for estimation | In-sample performance | Difference between in-sample and out-sample performance |


Prediction Bias & Variance¶
We want low value of both
If a measurement is biased, the estimate will include a constant systematic error

Bias-Variance Tradeoff¶
Usually U-Shaped
Each additional parameter adds the same amount of variance \(\sigma^2/n\), regardless of whether its true coefficient is large or small (or zero).
$$ \begin{aligned} \text{Variance} &= \sigma^2 \left[ \dfrac{1+k}{n} + 1 \right] \ & \approx O(k) \end{aligned} $$ Hence, we can reduce variance by shrinking small coefficients to zero
Tip¶
When using feature selection/LASSO regularization, stop one standard deviation > the optimal point, as even though bias has increased by a small amount, variance can be decreased a lot

VC Analysis¶
Let
- \(E_\text{in} =\) error on seen train data
- \(E_\text{test} =\) error on unseen test data
- \(E_\text{out} =\) theoretical error on the unseen population
- \(\vert h \vert =\) size of hypothesis, estimated through the number of Dichotomies
- \(\vert H \vert =\) size of hypothesis set, estimated through the number of Dichotomies
For test data, \(\vert H \vert = 1\), as it is not biased and we do not choose a hypothesis that looks good on it.
Pictorial Representation¶

IDK¶
Dichotomies¶
Prediction of hypothesis on data
No of dichotomies \(\le 2^n\)
Growth Function¶
counts the most dichotomies on \(n\) points $$ \begin{aligned} m_H(n) &= \max_{x_i} \vert H(x_i) \vert \qquad \forall i \in [1, n] \ \implies m_H(n) &\le 2^n \end{aligned} $$ The hypothesis set is said to “shatter” \(n\) points
Break Point¶
If no dataset of size \(n_b\) can be shattered by \(H\), then \(n_k\) is a break point for \(H\), ie Point at which you fail to get all possible dichotomies. This also implies that dataset of \(n > n_k\) cannot be shattered as well $$ m_H(k) = 2^k $$
VC Dimension¶
\(d_\text{VC}(H)\) is the most points \(H\) can shatter
\(d_\text{VC}(H)\) measures the effective number of parameters $$ \begin{aligned} d_\text{VC}(H) &= \arg \max_n m_H(n) = 2^n \ &= n_b-1 \end{aligned} $$
Independent of
- Learning algorithm
- Input distribution
- Target function
Dependent on
- Final hypothesis \(\hat f\)
- Training examples
- Hypothesis set
\(d_\text{VC}(H)\) is finite \(\implies\) \(\hat f \in H\) will generalize
Usually, \(d_\text{VC} \le\) no of parameters in the model
Sauer’s Lemma¶
Conclusion¶
| \(m_H(n)\) | |
|---|---|
| No break point | \(2^n\) |
| Any breakpoint | \(\sum_{r=0}^{d_\text{VC}(H)} n C_r\) Polynomial in \(n\) |
Hoeffding’s Inequality¶
But this is a very loose bound (better to loose, than incorrectly tight), as we assume that each hypothesis is disjoint

Vapnik-Chervonenkis Inequality¶
\(\delta\) is like the significance level
Why difference from Hoeffding’s?¶

Empirical observation: The bounded quantity has the same monotonicity as the bound
Generalization¶
Recommend Test Size¶
Rule of thumb to get good generalization $$ n_\text{test} \ge 10 \times d_\text{VC}(H) $$
Curse of Dimensionality¶
When \(k\) is very large, then the \(\vert H \vert\) gets very large and hence, generalization becomes very poor
Training Size¶
Generalization improves with size of training set, until a saturation point, after which it stops improving.
| More data \(\implies\) | |
|---|---|
| Parametric | asymptote to an error value exceeding Bayes error |
| Non-Parametric | better generalization until best possible error is achieved |
Generalization Bound vs Generalization Gap¶
| Generalization Gap | Generalization Bound | |
|---|---|---|
| Associated with | Model - Bias - Variance | Testing method - Test Set Size - No of trials |
Linear Regression¶
Consider true \(f = \text{Linear} + u; \quad u \sim N(0, \sigma^2_u)\)
- Best approximation error \(= \sigma^2_u\)
- Expected in-sample error \(= \sigma^2_u \left[1- \dfrac{k}{n} \right]\)
- Expected out-sample error \(= \sigma^2_u \left[ 1 + \dfrac{k}{n} \right]\)
- Expected generalization gap \(= 2 \sigma^2_u \left( \dfrac{k}{n} \right)\)

VC vs Bias-Variance¶

Scenarios¶
| Scenarios | Conclusion |
|---|---|
| Desired Error < Train Error | Underfitting/ Optimal |
| Train Error \(\approx\) Test Error \(\approx\) Desired Error Train Error < Test Error < Desired Error | Optimal |
| Train Error << Test Error Train Error < Desired Error < Test Error | Overfitting |
Fitting & Capacity¶
We can control the fitting of a model, by changing hypothesis space, and hence changing its capacity
| Underfitting | Appropriate-Fitting | Overfitting | |
|---|---|---|---|
| Capacity | Low | Appropriate | Low |
| Low Bias (Fitting Signal) | ❌ | ✅ | ✅ |
| Low Variance (Avoiding Noise) | ✅ | ✅ | ❌ |
| Implication | Acceptable | Optimal | Harmful |
| Steps to address | Increase model complexity Increase training data Remove noise from data Inc no of features | Cross-Validation More training data Feature Reduction Early Stopping Regularization | |
| Causes | - Small train set - Stochastic noise - Deterministic noise - Excessive model capacity |
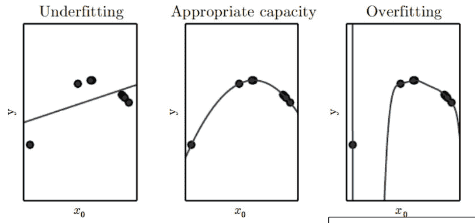
The capacity of a model increases with increased degree of polynomial
Interesting Note¶
Even if the target function is known to be of high complexity, for a small training dataset, a low capacity model will generalize better.



Unsupervised Learning¶
Harder to quantify than for supervised learning
If model is probabilistic, we can detect overfitting by comparing in-sample and out-sample log-likelihood
Detecting overfitting with larger datasets will be paradoxically harder
Clustering¶
Overfitting: Fitting small, local clusters rather than the true global clusters
Non-Probabilistic¶

Probabilistic Models¶
Log likelihood on in-sample and out-sample data
