Convolutional Neural Networks¶

Convolutional Neural Networks is a type of architecture that exploits special properties of image data and are used in computer vision applications.

Images are a 3-dimensional array of features: each pixel in the 2-D space contains three numbers from 0–255 (inclusive) corresponding to the Red, Green and Blue.

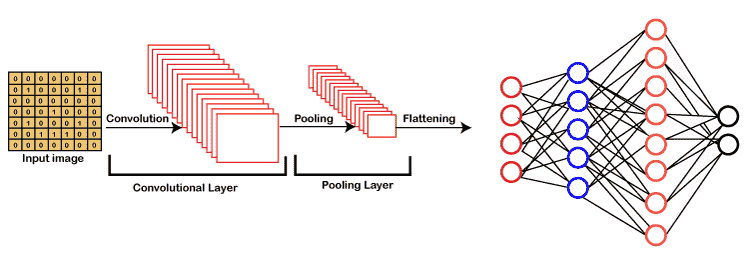
The first important type of layer that a CNN has is called the Convolution (Conv) layer. It uses parameter sharing and applies the same smaller set of parameters spatially across the image.

Essentially the parameters (i.e. weights) associated to the input remain the same but the input itself is different as the layer computes the output of the neurons at different regions of the image.

Hyperparameters of conv layers are - Filter size - corresponds to how many input features in the width and height dimensions one neuron takes in - Stride - how many pixels we want to move (towards the right/down direction) when we apply the neuron again

Then we have the pooling layer. The purpose of the pooling layer is to reduce the spatial size (width and height) of the layers. This reduces the number of parameters (and thus computation) required in future layers.

We use a fully connected layers at the end of our CNNs. When we reach this stage, we can flatten the neurons into a one-dimensional array of features.

We control output shape via padding, strides and channels

Very nice Youtube explanations. Watch this!

Advantages¶

• Universal visual feature extractor
• Can be used as building blocks in conjunction with architectures such as RNN/FCNN for complex tasks

Disadvantages¶

• High computational cost
• Large data requirements

Variables in this page¶

Principles¶

• Translation invariance
• Locality

Types of Layers¶

Notes¶

• Convolution and cross-correlation operations are slightly different, but it doesn’t matter if kernel is symmetric
• Since images are of different sizes, instead of using weight matrix of fixed size, convolution is applied various times depending on size of input
• 1 x 1 Convolutional Layer doesn’t recognize spatial patterns, but fuses channels
• \(\times\) is not multiplication; it is depth/no of activation maps

Example¶

The following shows convolution on with 0 padding and stride 1.

Convolutional Layer¶

Each filter in the conversation layer produces an “activation map”

Padding & Striding¶

Common Filters¶

Edge-Detection example

Smoothing

Object Detection¶

mAP = mean Average Precision

Advanced CNN¶

	RCNN	Fast-RCNN	Faster RCNN
Major idea	Region-Based	Do not recompute features for every box independently	Integrate bounding box proposals in CNN predictions
Steps	1. Generate category-independent region proposals (~2k) 2. Compute 4096-dimensional CNN feature vector from each region proposal 3. Classify regions w/ class- specific linear SVMs	1. Produce single convolutional feature map with several convolutional & max-pooling layers 2. Region of interest (RoI) pooling layer extracts fixed-length feature vector from region feature map	1. Compute proposals with a deep convolutional Region Proposal Network (RPN) 2. Merge RPN and Fast-RCNN into a single network
Advantages	Simple Improved mAP compared to RNN	Higher mAP Single end-to-end training stage No disk storage required	Cost-free region proposals
Disadvantages	Slow Multistage pipeline Disk storage required for feature caching Training is expensive	Proposals generation is computationally expensive
Flowchart

YOLO¶

You Only Look Once

Single CNN

No proposal for bounding box

Treat this as a single regression (not classification), straight from images pixels to bounding box coordinates and class probabilities

Steps¶

1. Residual block
2. Input split into 7x7 grids
3. Each cell trains a detector
   1. Detector needs to predict object’s class distributions
   2. detector has 2 bounding box predictor to predict bounding box and confidence scores
4. Generate probability for each grid having an object
5. Confidence Score = probability * IOU
6. Bounding box regression
7. IoU (Intersection over Union)
8. Non-max supression

Non-Max Supression¶

Algorithm Non-Max Supression
    Input: A list of proposal boxes B, corresponding confidence scores S and overlap threshold N
    Output:
        List of filtered proposals D

    select proposal with highest confidence score, remove it from B and add it to the fnal proposal list D
    Compare IOU of this proposal with all the proposal. If IOU > N, remove proposal from B

    more steps are there

IOU¶

Intersection Over Union

Let

• True bounding box be \(T\)
• Proposed bounding box be \(P\)

Interpretation¶

Popular Architectures¶

Operations¶

Padding
Pooling		Aggregate information
Striding
Depth-wise/ Grouped		Group together channels so that groups of channels in output only depend on corresponding groups of channels in input Enforce filter weight matrices to be block-diagonal
Dilations		Dilate convolution filter so that it covers more of the image Requires padding to ensure same size as input

Derivative¶

Adjoint $$ \begin{aligned} \bar v \dfrac{\partial \text{conv}(x, W)}{\partial x} &= \text{conv}(\bar v, \text{flip}(w)) \ \bar v \dfrac{\partial \text{conv}(x, W)}{\partial W} &= \end{aligned} $$

Comments